Recomendamos que esta clase se exponga previa a la explicación formal de los conceptos de divisor, número primo y número compuesto. Uno de los objetivos fundamentales de este tipo de exposiciones es que sean los mismos estudiantes los que, al final del tema, sean capaces de formalizar los conceptos.

En la exposición de este tema se intentará abordar los conceptos de divisor, número primo y número compuesto (todos ellos conceptos de la teoría de números) a través de conceptos y materiales geométricos.

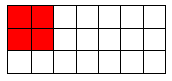
El concepto de número será entendido como el área de un rectángulo formado por pequeños cuadrados que se tomarán como la unidad.

Los estudiantes, al final del tema, deberán de ser capaces de reconocer los divisores de un número como el largo y el ancho del rectángulo que lo representa. Deberán, por tanto de ser capaces de distinguir entre los números primos y los compuestos.

Es esencial que el trabajo se haga por equipos
(Recomendamos que esté formado por 2 a 4 estudiantes)

CARTILLA DE AUTOEVALUACIÓN Esta cartilla la llenará cada estudiante tres veces en el transcurso de la exposición del tema. Es muy importante que el alumno anote la fecha de llenado para que después pueda compararlas. Fecha_______________________ Yo sé Completamente Bastante Un poco Nada Lo que es un rectángulo         Lo que es el ancho y el largo del rectángulo         Calcular el área de un rectángulo         Dividir         Lo que es el divisor de un número         Lo que es un número compuesto         Lo que es un número primo

	Por equipos. Los estudiantes deberán recortar de un papel cuadriculado (por ejemplo, una hoja de su cuaderno de matemáticas) 50 cuadrados iguales. Los cuadritos no deberán ser muy pequeños por lo que pueden hacerse de dos por dos. Algo así:
	Todo el grupo. (Hacer los dibujitos en el pizarrón) Es muy importante explicar al alumno lo siguiente: Cada cuadrito representará una unidad.
	Así el número 5, por ejemplo, se puede representar como:
	Un rectángulo de 5 por 1		Un rectángulo de 1 por 5
	El número 6 puede representarse de las siguientes maneras:
	Un rectángulo de 6 por 1	Un rectángulo de 1 por 6	Un rectángulo de 2 por 3	Un rectángulo de 3 por 2
	Por equipos. Buscar todas las representaciones en forma de rectángulo del número 7. Dibujarlas en el cuaderno.
	Por equipos. Buscar todas las representaciones en forma de rectángulo del número 12. Dibujarlas en el cuaderno.
	Todo el grupo. Cada equipo presentará los rectángulos que encontró en los pasos 3 y 4. Se discutirá si puede existir algún otro rectángulo o si los que se presentaron son realmente todos.
	Por equipos. Buscar todas las representaciones en forma de rectángulo de los números: 1, 2, 3, 4, 8, 9, 10, 11, 13, 14, 15, 16, 17, 18, 19 y 20. Dibujarlas, de forma ordenada en el cuaderno. Debajo de cada dibujo se escribirán los números que corresponden al largo y al ancho del rectángulo, así: 4 x 3 = 12