Capítulo 13
Números de Fibonacci y de Lucas
Tuvo esposas Fibonacci mas, |
Entre los matemáticos europeos de la Edad Media, el más grande de todos fue sin duda Leonardo de Pisa, más conocido por Fibonacci, que significa «hijo de Bonaccio» (véase la Figura 66).
|
|||
| Figura 66. Leonardo Pisano Fibonacci, nació en 1170, probablemente en Pisa, falleció en 1250, probablemente en Pisa |
A pesar de haber nacido en Pisa, como su padre era empleado en una factoría mercantil italiana asentada en Bougie, en Argelia, fue allí donde el joven Leonardo recibió su primera formación matemática, a cargo de maestros musulmanes. Pronto se dio cuenta de la enorme superioridad de la notación decimal indo arábiga (provista ya de cifras cuyos valores dependen de su posición, y de símbolo para el cero) sobre el engorroso sistema de numeración romana, empleado todavía en su país natal. La más conocida de sus obras, Liber abaci (literalmente , Libro del ábaco ) era en realidad un amplio tratado del sistema de numeración indo arábigo, mas sus razonamientos no parecieron causar demasiada impresión a los mercaderes italianos de la época. Con el tiempo, su libro llegó a ser, empero, la obra de máxima influencia entre todas las que contribuyeron a introducir en Occidente la notación indo arábiga. El Liber abaci fue concluido en Pisa en 1202; hasta nosotros ha llegado una edición revisada, de 1228, dedicada a un famoso astrólogo cortesano de la época.
No deja de ser irónico que Leonardo, cuyas aportaciones a la matemática fueron de tanta importancia, sea hoy conocido sobre todo a causa de un matemático francés del siglo pasado, Edouard Lucas, interesado por la teoría de números (y recopilador de una clásica obra de matemáticas recreativas, en cuatro volúmenes), quien encadenó el nombre de Fibonacci a una sucesión numérica que forma parte de un problema trivial del Liber abaci . Imaginemos, escribía Leonardo, un par de conejos adultos, macho y hembra, encerrados en un cercado, donde pueden anidar y criar. Supongamos que los conejos empiezan a procrear a los dos meses de su nacimiento, engendrando siempre un único par macho-hembra, y a partir de ese momento, cada uno de los meses siguientes un par más, de iguales características. Admitiendo que no muriese ninguno de los conejitos, ¿cuántos contendría el cercado al cabo de un año?
 |
||
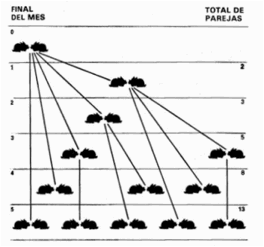
| Figura 67. Árbol genealógico de los conejitos de Fibonacci |
El gráfico arborescente de la Figura 67 nos muestra qué sucedería durante los cinco primeros meses. Es fácil observar que al término de cada mes los números de pares van formando la sucesión 1, 2, 3, 5, 8... donde cada número (como el propio Fibonacci hizo notar) resulta de sumar los dos que le anteceden. Al cabo de los 12 meses tendremos 377 pares de conejos.
Fibonacci no investigó la sucesión, que tampoco recibió ningún estudio serio hasta comienzos del siglo pasado. Hacia esa fecha los artículos dedicados a ella empezaron a proliferar, son palabras de un matemático, como los conejitos de Fibonacci. Lucas efectuó un profundo estudio de las llamadas sucesiones generalizadas de Fibonacci, que comienzan por dos enteros positivos cualesquiera y a partir de ahí, cada número de la sucesión es suma de los dos precedentes. Lucas dio el nombre de sucesión de Fibonacci a la más sencilla de estas sucesiones, a saber, 1, 1, 2, 3, 5, 8, 13, 21... (la inmediatamente más sencilla, 1, 3, 4, 7, 11, 18..., es hoy conocida por sucesión de Lucas). Tradicionalmente, la posición que cada número ocupa dentro de una sucesión se denota mediante un subíndice, y de esta forma,
| F 1 = 1 F 2 = 1 F 3= 2 |
y así sucesivamente. (Se da la lista de los primeros cincuenta números de Fibonacci en la Figura 68.) Fn denota el n -ésimo número de Fibonacci; Fn-1 es el número que antecede a Fn ; F 2n , es el número de Fibonacci cuyo subíndice es doble del de Fn , etc.
La sucesión de Fibonacci ha tenido intrigados a los matemáticos durante siglos, en parte a causa de su tendencia a presentarse en los lugares más inopinados, pero sobre todo, porque el más novel de los amateurs en teoría de números, aunque sus conocimientos no vayan mucho más allá de la aritmética elemental, puede aspirar a investigarla y descubrir curiosos teoremas inéditos, de los que parece haber variedad inagotable.
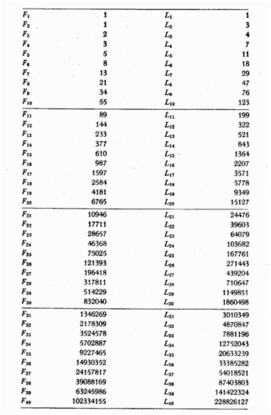 |
Figura 68. Los cuarenta números de Fibonacci y de Lucas
El interés por estas sucesiones ha sido avivado por desarrollos recientes en programación de ordenadores, ya que al parecer tiene aplicación en clasificación de datos, recuperación de informaciones, generación de números aleatorios, e incluso en métodos rápidos de cálculo aproximado de valores máximos o mínimos de funciones complicadas, en casos donde no se conoce la derivada.
Los resultados más clásicos acerca de estas sucesiones están resumidos en el Capítulo 17 del primer tomo de History of the Theory of Numbers , de Leonard Eugene Dickson. Los lectores interesados pueden consultar The Fibonacci Quarterty , que desde 1963 viene siendo publicada por la Fibonacci Association . Su redactor jefe es Verner E. Hoggatt, Jr., del San José State College de San José, Calif. La revista se ocupa, sobre todo, de las sucesiones generalizadas de Fibonacci y de otras sucesiones análogas (corno los llamados «números tribonacci», que son cada uno suma de los tres precedentes), aunque la revista está dedicada también «al estudio de enteros con propiedades especiales».
Seguramente la propiedad más notable de la sucesión de Fibonacci (válida también para las series generalizadas) sea que la razón entre cada par de números consecutivos va oscilando por encima y debajo de la razón áurea, y que conforme se va avanzando en la sucesión, la diferencia con ésta va haciéndose cada vez menor; las razones de términos consecutivos tienen por limite, en el infinito, la razón áurea. La razón áurea es un famoso número irracional, de valor aproximado 1,61803... que resulta de hallar la semisuma de 1 y la raíz cuadrada de 5. Hay abundante literatura (no siempre seria) dedicada a la aparición de la razón áurea y de la sucesión de Fibonacci tan relacionada con ella, en el crecimiento de los organismos y a sus aplicaciones a las artes plásticas, a la arquitectura e incluso a la poesía. George Eckel Duckworth, profesor de clásicas en la Universidad de Princeton, sostiene en su libro Structural Patterns and Proportions in Vergil's Aeneid (University of Michigan Press, 1962) que lo mismo Virgilio que otros poetas latinos de su época se sirvieron deliberadamente de la sucesión de Fibonacci en sus composiciones. Por mi parte, me he referido ya a estas cuestiones en un artículo anterior dedicado a la razón áurea, que puede verse en The Second Scientific American Book of Mathematical Puzzles and Diversions.
En el reino vegetal, la sucesión de Fibonacci hace su aparición más llamativa en la implantación espiral de las semillas en ciertas variedades de girasol. Hay en ellas dos haces de espirales logarítmicas, una de sentido horario, otra en sentido antihorario, como muestran las espirales sombreadas de la Figura 69.
Los números de espirales son distintos en cada familia, y por lo común, números de Fibonacci consecutivos. Los girasoles de tamaño medio suelen contener 34 y 55 espirales, pero hay flores gigantescas que alcanzan valores de hasta 89 y 144. Y en la sección de cartas a la redacción de The Scientific Monthly (noviembre de 1951), el geólogo Daniel T. O'Connell y su esposa dijeron haber encontrado en su granja de Vermont un girasol monstruo, con ¡144 y 233 espirales!
 |
Figura 69. Girasol gigante que contiene 55 espirales en sentido antihorario y 89 en sentido horario |
La íntima relación existente entre la sucesión de Fibonacci y la razón áurea queda de manifiesto en la siguiente fórmula explícita para el n -ésimo término de Fibonacci:
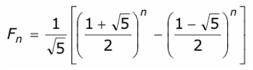 |
Esta expresión da exactamente el n -ésimo número de Fibonacci (al desarrollarla, las v5 se cancelan), pero para números F n de lugar muy avanzado es fastidiosa de utilizar, si bien pueden conseguirse buenas aproximaciones mediante logaritmos. Otra fórmula mucho más sencilla para el n -ésimo número de Fibonacci consiste en dividir entre la raíz cuadrada de 5 la n -ésima potencia de la razón áurea. Redondeando el número así obtenido al entero más cercano resulta también el valor entero exacto del número buscado. Ambas fórmulas son «explícitas», pues conocido n dan directamente el valor de Fn Un «procedimiento recursivo» consiste en una serie de etapas, cada una de ellas dependiente de las anteriores. Si para calcular el n- ésimo número de Fibonacci se van sumando pares de términos consecutivos hasta alcanzarlo, se estará procediendo iterativamente, o por recurrencia. Al definir el término Fn como suma de los dos términos que le anteceden estamos dando un ejemplo sencillo de fórmula recurrente.
La fórmula que da exactamente el término general de la sucesión de Lucas es
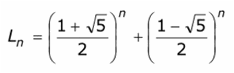 |
pero, como sucedía con los números de Fibonacci, hay un procedimiento mucho más sencillo para hallar el n- ésimo número de Lucas. Basta elevar la razón áurea a la n- ésima potencia y redondear al entero más cercano.
Dado un número cualquiera de la sucesión de Fibonacci, para calcular el término siguiente no es preciso conocer su índice. Sea A, el término dado. El siguiente viene dado por
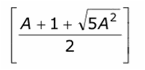 |
donde los corchetes indican que es necesario tomar la parte entera de la expresión, es decir, el entero más cercano por defecto. Esta misma fórmula da el número de Lucas consecutivo a cualquiera de su serie, con tal de que sea mayor que 3.
En toda sucesión de Fibonacci generalizada la suma de los n primeros términos es siempre F n-2 , menos el segundo término de la serie. Gracias a ello podemos realizar un truco de cálculo súper-rápido. Se le pide a otra persona que escriba dos números cualesquiera, y que vaya formando después tantos términos de la sucesión generalizada que engendran como desee. Pídale después que separe con un trazo dos cualesquiera de éstos. Instantáneamente puede usted darle la suma de todos los números situados antes de la raya. Basta con fijarse en el segundo número situado al otro lado de la raya, y restarle el segundo término de la sucesión. De tratarse de la sucesión de Fibonacci ordinaria se restaría 1; de ser la sucesión de Lucas, restaríamos 3.
Citaremos ahora algunas conocidas propiedades de la sucesión de Fibonacci ordinaria. Pocas de ellas son costosas de demostrar, y desde luego, todas son casos particulares de teoremas válidos para sucesiones generalizadas. Para abreviar, llamaremos números F a los números de Fibonacci.
1. El cuadrado de cada número F se diferencia en 1 del producto de los dos números F situados a cada uno de sus lados. Conforme se avanza en la sucesión, esta diferencia va siendo alternativamente positiva y negativa. (En los números de Lucas, la diferencia, también constante, vale 5.) En el Capítulo 8 de mi libro Mathematics, Magic and Mystery puede verse una famosa paradoja de disección geométrica donde este teorema tiene papel fundamental. En las sucesiones de Fibonacci generalizadas la diferencia constante es
| + ( F22 , F12 – F 1 F2 ). |
2. La suma de los cuadrados de dos números F consecutivos cualesquiera, F n 2 más F n+12 , es F 2n+1 . Puesto que el último de estos números es forzosamente de índice impar, resulta de este teorema que al escribir en sucesión los cuadrados de los números de Fibonacci, las sumas de los pares de cuadrados consecutivos formarán la sucesión de números F con subíndice impar.
3. Cualesquiera cuatro números F consecutivos A, B, C, D verifican la siguiente identidad:
| 2 2 | ||
| C – B = A x D. |
4. La sucesión de las últimas cifras de los números de Fibonacci tiene período 60. Si se toman las dos últimas cifras, la sucesión tiene período 300. Para la sucesión formada a partir de las tres últimas cifras el periodo es ya 1.500; para cuatro, el período tiene 15.000 cifras, para cinco, 150.000, y así sucesivamente.
5. Para cada entero m hay una colección infinita de números de Fibonacci exactamente divisibles por m , de los cuales al menos uno se encuentra entre los 2 m primeros términos de la sucesión. No ocurre igual para la sucesión de Lucas. Por ejemplo, ninguno de los números de la sucesión de Lucas es divisible entre 5.
6. El tercero de cada tres números de la sucesión de Fibonacci es divisible por 2; al contarlos de cuatro en cuatro, el cuarto es divisible por 3. El quinto de cada cinco es divisible por 5; el sexto de cada seis, divisible entre 8, y así sucesivamente, siendo los divisores números F en sucesión. Dos números de Fibonacci consecutivos (y lo mismo ocurre con los números de Lucas) son primos entre sí, es decir, no tienen más divisor común que el 1.
7. A excepción de 3, todo número F que sea primo tiene subíndice primo. (Por ejemplo, 233 es primo y porta subíndice 13, también primo.) Dicho de otra forma, si el subíndice es compuesto, también lo será el número de Fibonacci correspondiente. Pero, cuidado, la recíproca no es cierta. Hay números de Fibonacci con subíndices primos que son números compuestos. El primer ejemplo de este tipo es F 19 , que vale 4.181. Aunque el subíndice es número primo, 4.181 se descompone en 37 por 113.
Si el teorema recíproco hubiera sido verdadero en todos los casos, habría quedado resuelta la más importante de las cuestiones sobre sucesiones de Fibonacci todavía pendientes: ¿existirá una infinidad de números primos en la sucesión de Fibonacci? Sabemos que la colección de números primos es infinita, y por consiguiente, si todo F -número que portase subíndice primo fuese primo, habría también una infinidad de números primos en la sucesión de Fibonacci. Hoy por hoy se ignora si existe un número primo máximo entre los F -números. También subsiste la misma cuestión para los números de Lucas. El más grande de los números F primos hoy conocidos es F 9 , que consta de 119 cifras. El mayor de los números L primos descubiertos es L 353 , formado por 74 cifras.
8. Con las excepciones triviales de 0 y 1 (tomando 0 = F 0 ) entre los números de Fibonacci hay solamente un cuadrado perfecto, F 12 = 144, muy curioso, pues su valor es cuadrado de su subíndice. La existencia o inexistencia de cuadrados mayores que 144 fue problema abierto hasta fecha tan reciente como 1963. En ese año la cuestión quedó resuelta por John H. E. Cohn, del Bedford College , de la Universidad de Londres. El mismo demostró también que los únicos cuadrados perfectos contenidos en la sucesión de Lucas son 1 y 4.
9. En la sucesión de Fibonacci hay solamente dos cubos, 1 y 8; en la de Lucas, el único cubo perfecto es 1. (Véase «On Fibonacci and Lucas Numbers Which Are Perfect Powers», por Hymie London y Raphael Finkeistein, en The Fibonacci Quarterty , vol. 77, diciembre de 1969, pp. 476-81).
10. El inverso del decimoprimero número de Fibonacci, 89, puede ser engendrado a partir de esta sucesión, empezando por 0 y sumando después como se muestra:
 |
La lista de propiedades de la sucesión de Fibonacci bastaría para llenar un libro. Otro tanto puede decirse de sus aplicaciones en Física y Matemáticas. Leo Moser ha estudiado las trayectorias de rayos luminosos que inciden oblicuamente sobre dos láminas de vidrio planas y en contacto. Los rayos que no experimentan reflexión alguna atraviesan ambas láminas de sólo una forma (véase la Figura 70).
|
Para los rayos que sufren una reflexión hay dos rutas posibles; cuando sufren dos reflexiones, las trayectorias son de tres tipos, y cuando sufren tres, de cinco. Al ir creciendo el número n de reflexiones, el número de trayectorias posibles va ajustándose a la sucesión de Fibonacci: para n reflexiones, el número de trayectorias es F n+2 .
La sucesión puede utilizarse de forma parecida para contar el número de distintas rutas que puede seguir una abeja que va recorriendo las celdillas hexagonales del panal (véase la Figura 71).
Figura 71. La abeja puede caminar hasta la celdilla n de F n+2 maneras |
La hilera de casillas puede prolongarse indefinidamente hacia la derecha. Supondremos que la abeja se dirige siempre a una celdilla contigua y a la derecha de la que ocupa. Poco cuesta probar que hay sólo una ruta hasta la casilla 0, dos hasta la número 1, tres hasta la 2, cinco itinerarios que conduzcan a la 3, y así sucesivamente. Al igual que antes, el número de trayectos es F n+2 , donde n es el número de casillas del problema.
Y ya que viene a cuento, las abejas machos, o zánganos, no tienen padre. C. A. B. Smith ha hecho notar que cada zángano tiene madre, 2 abuelos (los padres de la madre), 3 bisabuelos (y no cuatro, pues el padre de la madre no tuvo padre), 5 tatarabuelos, y así sucesivamente, en sucesión de Fibonacci.
David Klamer ha mostrado que los números de Fibonacci expresan de cuántas maneras podemos construir con dominós (rectángulos de tamaño 1 x 2) rectángulos de dimensión 2 x k . Hay sólo una manera de formar el rectángulo 2 x 1; 2 maneras de construir el cuadrado de 2 x 2; 3 para el rectángulo de 2 x 3; 5 para el de 2 x 4, y así sucesivamente.
Fijémonos ahora en el nim de Fibonacci, juego inventado hace algunos años por Robert E. Gaskell, y consistente en ir retirando cuentas de una pila que inicialmente contiene n fichas. Los jugadores actúan por turno. En la primera jugada no es lícito retirar la pila completa, aunque sí en las sucesivas, siempre que se respeten las siguientes reglas: en cada turno es forzoso retirar al menos una ficha, y ningún jugador puede tomar más del doble del número de fichas que haya tomado su oponente en la jugada anterior. Por tanto, si un jugador se lleva tres, el siguiente no podrá retirar más de seis. Gana la partida quien retire la última ficha.
Resulta que si n es número de Fibonacci el segundo jugador puede ganar siempre; en los demás casos, es el primero quien puede conseguir, si juega bien, siempre la victoria. Si una partida comienza con 20 fichas (que no es número de Fibonacci), ¿cuántas debe retirar el primer jugador para estar seguro de ganar?
El segundo problema se refiere a un truco de cálculo relámpago muy poco conocido. Vuélvase de espaldas, y pídale a un amigo que escriba un par de enteros positivos cualesquiera (uno debajo del otro), que los sume y obtenga un tercero, que debe describir debajo del segundo; que sume los dos últimos números y obtenga un cuarto, prosiguiendo de esta forma hasta formar una columna de diez números. Es decir, ha de escribir los diez primeros términos de una sucesión generalizada de Fibonacci, donde cada término es suma de los dos que le preceden, exceptuados los dos primeros, que son arbitrarios. Hecho esto, usted se vuelve, traza una raya por debajo de los diez sumandos, e inmediatamente escribe la suma.
La clave consiste en multiplicar por 11 el séptimo de los números a sumar, operación que fácilmente se realiza de cabeza. Supongamos que el séptimo número sea 928. Anotamos ya la cifra 8, que será la última cifra de la suma. Sumamos 8 y 2, y obtenemos 10. Escribimos en la suma un 0 inmediatamente al lado del 2, y llevamos 1. La suma del siguiente par de cifras, 9 y 2, es 11. Añadimos el 1 que arrastrábamos, y tenemos 12. Escribirnos el 2 a la izquierda del 0 en la suma, y seguimos llevando 1, que sumaremos al 9, y en la suma anotamos 10 a la izquierda del 2. La suma, ya terminada, es 10.208. En resumen, se suman las cifras por pares de derecha a izquierda, llevando 1 cuando sea necesario, y terminando con la última cifra de la izquierda.
¿Sabrá el lector demostrar que la suma de los 10 primeros números de una sucesión de Fibonacci generalizado es siempre 11 veces el séptimo término?
Apéndice
Los números de «Tribonacci» (1, 1, 2, 4, 7, 13, 24, 44, 81, ...) fueron así bautizados por el joven y brillante matemático Mark Feinberg, quien publicó un artículo sobre ellos en The Fibonacci Quarterly , (octubre de 1963), cuando sólo contaba 14 años. Su carrera en la Universidad de Pennsylvania quedó cercenada en 1967, en su segundo año de universidad, al resultar muerto en un accidente de motocicleta.
En su artículo sobre números de Tribonacci, Feinberg puso de relieve que al ir avanzando en la sucesión, la razón entre términos adyacentes converge hacia 0,5436890126.... y más exactamente, hacia la raíz real de la ecuación x 3 + x 2 + x , 1 = 0. Podemos generalizar más y estudiar sucesiones donde cada término sea suma de los cuatro (números de Tetranacci), cinco, seis, etc., números que lo anteceden. En todas esta sucesiones, la razón de cada término al siguiente tiene un límite; al ir aumentando el número de términos a sumar, la razón límite disminuye, tendiendo a su vez hacia 0,5. Tal generalización había sido publicada hacia 1913 por Mark Barr. (Véase mi Second Scientific American Book of Mathematical Puzzles and Diversions , página 101.)
«La notación de Fibonacci» (que presentamos en la solución del primer problema) consiste en expresar unívocamente cada entero en suma de números de Fibonacci; esta descomposición tiene importancia en técnicas de clasificación mediante ordenador. En mi sección de «Juegos Matemáticos» de Scientific American de abril de 1973 puede verse un método para emplear el «ábaco de Napier» (dispositivo de cálculo muy poco conocido, cuyo inventor ideó también los «dados de Napier») para cálculos en notación de Fibonacci. Con respecto a la importancia de la notación de Fibonacci en la estrategia de juego del «nim de Wythoff», puede verse mi artículo de «Juegos Matemáticos» en el número de mayo de 1977 de INVESTIGACIÓN Y CIENCIA (edición en español de Scientific American ). Y respecto a la relación entre el triángulo de Pascal (o de Tartaglia) y la sucesión de Fibonacci, véase el Capítulo 15 de mi Carnaval Matemático (LB 778, Alianza Editorial).
Las sucesiones de Fibonacci y Lucas están interrelacionadas por docenas de fórmulas sencillas. Por ejemplo, el n -ésimo número de Lucas es igual a F n-1 + F n+1 . El producto de F n y L n es igual a F 2n . La siguiente ecuación diofántica
| 5 x 2 + 4 = y2 |
tan sólo tiene soluciones enteras cuando x es un número de Fibonacci e y sea el correspondiente número de Lucas.
Las sucesiones de Fibonacci y Lucas tienen en común los números 1 y 3. ¿Habrá otros números mayores, comunes a las dos sucesiones? La respuesta resulta negativa. Véase la nota de Martin D. Hirsch sobre «Additive Sequences», en Mathematies Magazine , vol. 50, noviembre de 1977, página 264.
Como ya he mencionado, el más notable de los problemas abiertos concernientes a sucesiones de Fibonacci es el de si contienen o no colecciones infinitas de números primos. En una sucesión de Fibonacci generalizada, si los primeros números son divisibles ambos por un mismo número primo, todos los términos posteriores lo serán también, y es evidente que tales sucesiones no podrán contener más de un número primo. Supongamos, pues, que los dos primeros números sean primos entre sí (esto es, que su único común divisor sea 1). ¿Podrán existir sucesiones generalizadas que no contengan absolutamente ningún número primo?
El primero en resolver esta cuestión fue R. L. Graham, en «A Fibonacci-like Sequence of Composite Numbers», en Mathematics Magazine , vol, 57, noviembre de 1964, pp. 322-24. Existe una infinidad de sucesiones así, pero la mínima (en el sentido de serlo sus dos primeros números) es la que empieza por:
1786772701928802632268715130455793,
1059683225053915111058165141686995.
Soluciones
El primer problema consiste en hallar la jugada de apertura correspondiente a la estrategia vencedora en una partida de « nim de Fibonacci», sabiendo que el montón de fichas consta de 20 piezas. Como 20 no es número de Fibonacci, si el primer jugador actúa con inteligencia, es seguro que ganará la partida. Para determinar la estrategia vencedora, se descompone el número 20 en suma de números de Fibonacci, comenzando por el mayor posible, 13, sumando después el máximo posible, 5, y después el siguiente, 2. Así que 20 = 13 + 5 + 2 es la descomposición buscada. Todo entero positivo puede ser expresado de forma única como suma de números de Fibonacci; tal descomposición no podrá nunca contener números de Fibonacci consecutivos. Los números F quedan expresados por un solo número: ellos mismos.
El último número, 2, es el número de piezas que debe retirar el primer jugador para ganar. El segundo jugador queda imposibilitado, por las reglas del juego, para tomar más del doble de 2; por consiguiente, no puede reducir la pila (que tiene ahora 18 cuentas) al número de Fibonacci más cercano, que es 13. Supongamos que decida retirar cuatro piezas; la pila contendrá entonces 14 piezas, número que se expresa como 13 + 1 en suma de dos números de Fibonacci, y el primer jugador deberá entonces tomar 1 pieza. Prosiguiendo con esta estrategia, es seguro que logrará tomar la última ficha, y con ella, ganar la partida.
Si el número de inicial de piezas fuera número de Fibonacci, por ejemplo, 144, es seguro que el segundo jugador podrá ganar. Es verdad que el primer jugador puede retirar 55 piezas, dejando 89, que es el siguiente número de Fibonacci, pero entonces el segundo jugador puede ganar inmediatamente, retirando lícitamente las 89 piezas restantes, pues 89 es menor que el doble de 55. El primer jugador se ve entonces precisado a dejar un número de piezas no perteneciente a la sucesión de Fibonacci, y el segundo jugador consigue ganar aplicando la estrategia que acabo de explicar. (Véase Donald E. Knuth, Fundamental Algorithms , Addison-Wesley, 1968, página 493, Ejercicio n. 37, y también, «Fibonacci Nim», por Michael J. Whiniham, en The Fibonacci Quarterly , vol. 1, n. 4, diciembre de 1963, pp. 9-13.)
Para demostrar que en toda sucesión de Fibonacci generalizada la suma de los 10 primeros términos es siempre 11 veces el séptimo, sean a y b los dos primeros números. Los 10 números, y su suma, pueden ser representados como vemos en la Figura 72. Es evidente que la suma es 11 veces el séptimo número. Notemos también que los coeficientes de a y b de estos desarrollos forman sendas sucesiones de Fibonacci.
Figura 72. Solución al problema de Fibonacci |
Referencia:
GARDNER, Martin. Números de Fibonacci y de Lucas, Capítulo 13. En libro electrónico: Circo Matemático. Disponible en: http://www.librosmaravillosos.com/circomatematico/capitulo13.html